
Pozrite sa na
Podporili nás

Zadania seminára STROM, 41. ročník - Letný semester
Vzorové riešenia 1. série nájdeš v časopise STROM-41-5
Vzorové riešenia 2. série nájdeš v časopise STROM-41-6
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Termín série: 27. marec 2017 22:00:00
1. Štvorec s obsahom $5$ je pokrytý $9$ mnohouholníkmi s obsahom $1$. Dokážte, že existujú dva mnohouholníky, ktorých prienik má obsah aspoň $1/9$.
2. Na tabuli sú napísané čísla $1,\ 2,\ \dots,\ 17$. Čísla zotierame tak, že z nezotretých čísel si vyberieme ľubovoľné číslo $k$ a zotrieme všetky delitele čísla $k+17$. Je možné zmazať všetky čísla?
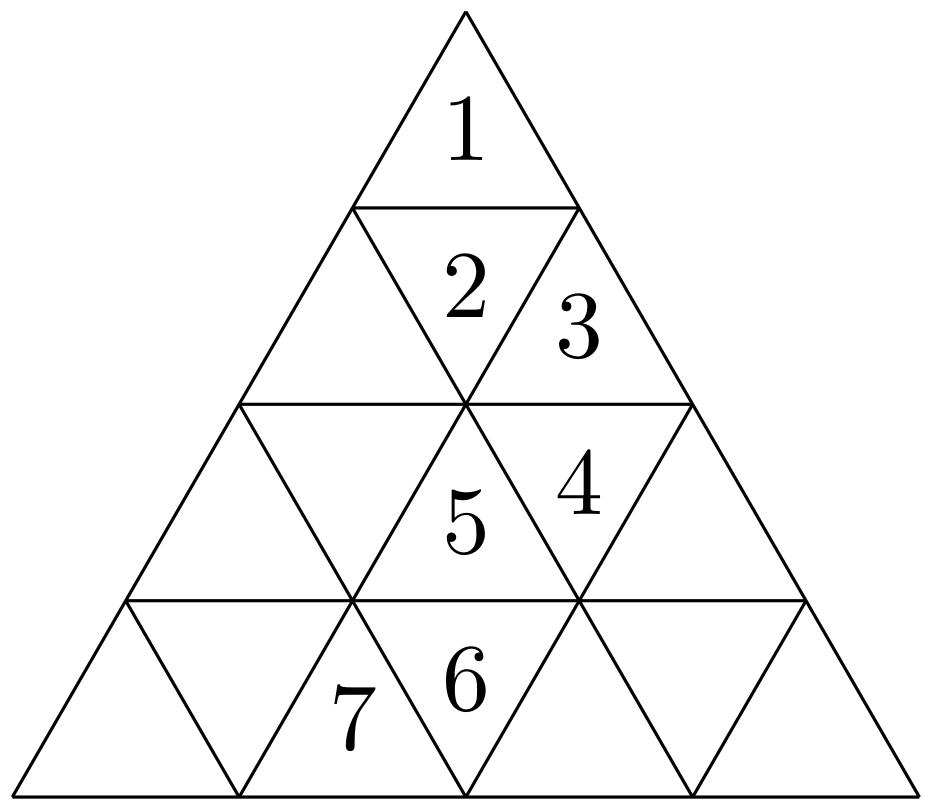
3. Rovnostranný trojuholník je rozdelený na $n^2$ zhodných trojuholníkov (napr. obrázok pre $n=4$). Niektoré z nich sú očíslované číslami od $1$ do $m$ tak, že susedné čísla sú vpísané do susedných trojuholníkov - majú spoločnú stranu. Dokážte, že $m \leq n^2 - n + 1$.

4. Biologička Janka pozoruje chameleóna, ktorý chytá muchy. Chameleón má však prešpekulované pravidlá, ako bude pri chytaní múch oddychovať. Pred prvou chytenou muchou oddychuje $1$ minútu. Pred každou $2m$-tou muchou oddychuje toľko minút, ako oddychoval pred $m$-tou muchou. Pred každou $(2m+1)$-ou muchou oddychuje o minútu viac, ako oddychoval pred $m$-tou muchou. Keď skončí niekoľko minútový oddych, chameleón okamžite chytí muchu a opäť začne oddychovať. Zistite:
- Koľkátu muchu chytil chameleón po tom, čo prvý krát oddychoval $7$ minút bez chytania?
- Po akom dlhom oddychu chytil chameleón svoju $2047$-mu muchu?
5. Je daný tetivový päťuholník $ABCDE$ taký, že $|AB| = |BC|$. Bod $P$ je priesečník priamok $BE$ a $AD$ a bod $Q$ je priesečník priamok $CE$ a $BD$. Priamka určená bodmi $PQ$ pretne opísanú kružnicu v bodoch $X,\ Y$. Dokážte $|BX| = |BY|$.
6. Nech $a,b,c$ sú kladné reálne čísla také, že $abc=1$. Dokážte, že $$\frac{a+b+c+3}{4}\ge\frac1{a+b}+\frac1{a+c}+\frac1{c+b}.$$
Vzorové riešenia 1. série nájdeš v časopise STROM-41-5
Vzorové riešenia 2. série nájdeš v časopise STROM-41-6
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Termín série: 9. máj 2017 22:00:00
1. Dokážte, že ak $p$, $q$ sú kladné celé čísla čísla, tak kladným celým číslom je aj $$\frac{10^{p+q}+2\cdot10^q+2\cdot10^p+4}{36}.$$
2. Dokážte, že v ľubovoľnom konvexnom mnohouholníku (okrem rovnobežníka) možno vybrať tri strany tak, aby priamky nimi určené tvorili trojuholník, v ktorom je daný mnohouholník obsiahnutý.
3. V každom vrchole štvorca máme $1$ kamienok a v každom kroku môžeme previesť nasledujúcu operáciu: z ľubovoľného vrcholu zoberieme niekoľko kamienkov (najviac toľko, koľko ich tam je) a pridáme dvakrát viac kamienkov na niektorý zo susedných vrcholov. Je to možné robiť tak, aby sme na konci vo vrcholoch dostali (zaradom po obvode) $2016$, $2015$, $2017$ a $2016$ kamienkov?
4. Nájdite všetky kladné celé čísla $n$, ktoré sa nedajú zapísať v tvare $n=[a,b]+[b,c]+[c,a]$, pričom $a,\ b,\ c$ môžu byť ľubovoľné kladné celé čísla. Pozn: $[a,b]$ označuje najmenší spoločný násobok čísel $a,b$.
5. Na odvesnách $AC$ a $BC$ pravouhlého trojuholníka $ABC$ sú zvolené postupne body $K$ a $L$ a na prepone bod $M$ tak, že platí $|AK| = |BL| = a$, $|KM| = |LM| = b$ a uhol $KML$ je pravý. Dokážte, že $a = b$.
6. Univerzálnou postupnosťou čísel $1,\ 2,\ \dots, n$ nazveme takú (konečnú) postupnosť týchto čísel, že vyčiarknutím niektorých jej členov z nej dostaneme ľubovoľnú permutáciu týchto čísel (napr. $1,\ 2,\ 3,\ 1,\ 2,\ 3,\ 1$ je univerzálna postupnosť čísel $1,\ 2,\ 3$, lebo ľahko preveríme, že všetky permutácie, t.j. $1,2,3;$ $1,3,2;$ $2,1,3;$ $2,3,1;$ $3,1,2;$ $3,2,1$ vzniknú vyčiarknutím niektorých jej členov). Nájdite najkratšiu univerzálnu postupnosť čísel $1$, $2$, $3$ a potom aj čísel $1$, $2$, $3$, $4$ a dokážte, že kratšie neexistujú.
Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...